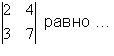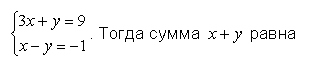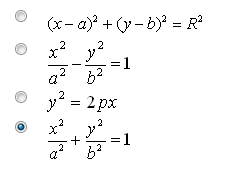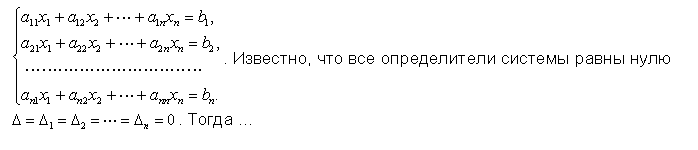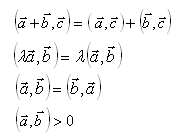Содержание
- Ранг матрицы
- Алгебраическое дополнение элемента
- А23 = 12
- Произведение матриц
- — правильно
- Если все элементы одной строки прямоугольной матрицы А размерности n x m умножить на два то ранг матрицы А …
- Верное соотношение
- — правильно
- Значение определителя
- 2
- Взаимное расположение прямых 4x — 2y — 6 = 0 и 8x — 4y — 2 = 0 на плоскости – прямые …
- Пусть х и у решения системы
- Среди приведенных ниже уравнений указать уравнение эллипса
- Пусть прямая задана нормальным уравнением x sinα + y sinα – p = 0. Верное утверждение
- Дана линейная система
- Уравнение прямой заданной точкой А(2,1) и направляющим вектором
- Найти скалярное произведение векторов
- Уравнение прямой проходящей через точку M(1;2) и образующей с осью Ох угол в 45º имеет вид …
- Свойство скалярного произведения, которое не имеет места
- Ответ:
Ранг матрицы
- 5
- 2
- 4
Алгебраическое дополнение элемента
А23 = 12
- А23 = -34
- А23 = 34
- А23 = -12
Произведение матриц
 — правильно
— правильно
Если все элементы одной строки прямоугольной матрицы А размерности n x m умножить на два то ранг матрицы А …
- увеличится на 2
- не изменится
- увеличится в два раза
Верное соотношение
 — правильно
— правильно
Значение определителя
2
- 4
- 5
- 3
Взаимное расположение прямых 4x — 2y — 6 = 0 и 8x — 4y — 2 = 0 на плоскости – прямые …
- параллельны
- пересекаются
- перпендикулярны
- совпадают
Пусть х и у решения системы
- 4
- 7
- 5
- 6
Среди приведенных ниже уравнений указать уравнение эллипса
Пусть прямая задана нормальным уравнением x sinα + y sinα – p = 0. Верное утверждение
- Если ОА – перпендикуляр, восстановлены из начала координат к прямой, то α — угол образованный перпендикуляром ОА с осью Ох
- Если ОА – перпендикуляр, восстановлены из начала координат к прямой, то α — длинна этого перпендикуляра
- р — величина отрезка, отсекаемого прямой на оси Ох
- α — угол наклона прямой к положительному направлению оси Ох
Дана линейная система
- система имеет бесчисленное множество решений
- система не имеет решений
- система имеет единственное решение
- о наличии решений ничего сказать нельзя (система может как иметь так и не иметь решения)
Уравнение прямой заданной точкой А(2,1) и направляющим вектором
- 5x — 3y — 7 = 0
- 3x + y — 7 = 0
- 4x — 2y — 6 = 0
- 6x — y — 11 = 0
Найти скалярное произведение векторов
- 6
- 6
- 6
Уравнение прямой проходящей через точку M(1;2) и образующей с осью Ох угол в 45º имеет вид …
- 2x — y = 0
- 3x — 2y + 1 = 0
- x — 2y + 3 = 0
- x — y + 1 = 0
Свойство скалярного произведения, которое не имеет места
Ответ:



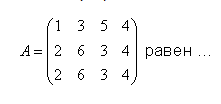
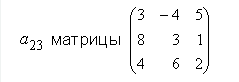
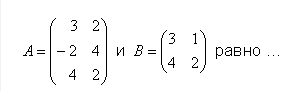
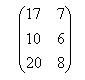 — правильно
— правильно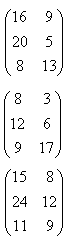
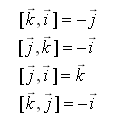 — правильно
— правильно